In my post on the correlation between squad cost and table position a regression model was developed to quantify the relationship between the two. Since then, there have been many questions asked about the regression analysis.
- How much would Liverpool have to spend to have a shot at qualifying for Champions League?
- Considering the model captures 70% of the variation between the two data sets, how much does Liverpool need to spend to “safely” have a shot at Champions League?
- What were the actual predicted, unclipped finish positions for 2010-2011?
- Why focus on the Sq£ metric rather than £XI?
The Easy Stuff: The Full Prediction Table and Why MSq£ Is Used
First, let’s address the answers to the easier questions before diving into the new concepts.
Why focus the original analysis on Sq£ rather than the £XI? As was stated in the original post, there were several factors that went into that decision:
- To determine the most basic relationship between financial expenditures and table position, analysis must follow the order of events. That is, a transfer must first take place, then a wage negotiated, then a player can put in time on the pitch and generate utilization statistics. Thus, the original analysis first looked at overall transfer expenditures to see if there was a relationship. If there is one, likely root cause correlation has been established.
- As £XI requires utilization before it is populated with a value, it cannot be used as a forward looking, predictive metric to gauge future performance.
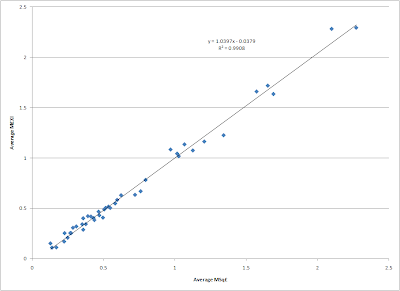
Any regression study of table position versus M£XI is going to be nearly identical to the MSq£ regression in the original study. While utilization rates over time may vary due to managerial issues, injuries, illness, etc. the average tendency is that spending more on the squad gives a club about the same advantage in the average cost of the talent that appears in any match in a season.
That’s not to say the spending on squad and the XI on the pitch is equal. In fact, the graph below indicates that in the eighteen years of the Premier League the disparity between the cost of the squad and the cost of the talent on the pitch has been growing (click image to enlarge).
As can be observed, the average Sq£ rose by about a £2.34M per season (Note: the rate of increase drops dramatically to £1.55M/season if the first three years of 22 teams per season are removed from the data set). At the same time the ratio of the season average £XI to average Sq£ has been dropping by about 1% every three years. This means that while one must spend multiples of the league average in Sq£ to compete for top table positions, an ever increasing amount of the squad expenditures will not see time on the pitch. This is yet another confirmation that financially rich clubs have an advantage over poorer ones.
Next, we consider what happens when the predicted table position from the MSq£ regression equation is not clipped at 1.0. The table below shows the unclipped and clipped values for predicted 2010/11 table position based upon each club’s 2010/11 MSq£ and sorted in ascending order of current table position. The table positions were taken as of January 18, 2011 from statto.com.
One can now begin to understand how out-of-the-norm Chelsea’s, Manchester City’s, and Manchester United’s 2010/11 spending is – they each have a predicted finish below zero. To be fair, this is a bit of an effect that Stefan Szymanski noticed in his own data set as well as the Transfer Price Index: the expenditures and table positions of such teams over time have led the regression models to modestly over predict the squad wage and transfer costs required for a top spot in the league.
The Advanced Stuff: Using Prediction Intervals to Predict the MSq£ Required for Champion’s League Qualification
One intrepid reader of my last blog post asked how one might calculate the Sq£ required for Liverpool to achieve fourth place given the regression equation, as well as the minimum amount required to have a reasonable chance at such a spot. Luckily, an advanced regression concept can help us answer those questions.
The regression equation predicts a club must spend 1.98 times the league average to achieve a fourth place position. Given Liverpool’s current MSq£ of 1.35 and the 2010-2011 average Sq£ of £115.7M, the Reds would have to increase their Sq£ by £73.6M to reach the magical MSq£ of 1.98. However, regression analysis, like all statistical theory, is really all about the underlying distribution of data upon which it is built. The regression equation we see in a graph is technically a “least squares” analysis, where the software constructs a mathematical equation that minimizes the square of the differences between the regression’s predicted values and the actual values in the data set (aka “minimizing the square of the residuals”). The resulting line and the equation describing it can be thought of as a 50/50 answer – the value of any single past or future observation has a 50% chance of being above the regression line or a 50% chance below it. We can think of the regression line as the likely average value.
Luckily, advanced statistical packages allow us to understand the distribution of the expected y-axis (or response) values (i.e. table position) for a given x-axis (or predictor) value (i.e. MSq£). These distributions are called prediction intervals (PI), and are used to understand the range of values (table position) that can be expected for an individual future observation (MSq£). Prediction intervals are communicated as percentages, and are centered on the regression line. Thus, a 50%PI represents the bounds of 50% of the expected finishing positions over time for a given MSq£, and is expressed as the maximum and minimum table position (the bounds) in that distribution. Those bounds are the data points that are 25% above and 25% below the original regression line. Prediction intervals can be calculated along the entire range of predictors (MSq£) to generate bounds around the regression line.
A common use of PI’s is to identify outliers in the data set. This is done by calculating the 95% PI lines for the distribution and then identifying which pieces of data from the overall data set fall outside the lines. Any point that falls outside of the lines represents 5% of the data, thus has a low chance of occurring. A plot of table position vs. MSq£ can be found below. The original regression equation is found with its 95% PI lines (dashed) (click image to enlarge).
Only two teams fall outside the 95% PI, and thus are considered outliers. Both fell above the upper line, indicating they grossly underperformed versus the regression equation. Both teams played in the 22 team era of the league, with both being relegated rather quickly.
The first, Swindon Town, spent only 0.25 times the average Sq£ in their one and only season in the Premier League (1993-1994). Combine that inexpensive squad with the fact that their manager departed for greener pastures as soon as promotion from the Championship was achieved, and it’s little wonder they set a standard of futility few have surpassed (including conceding 100 league goals).
The second, Oldham Athletic, were inaugural members of the Premier League and lasted two seasons before they were relegated. They spent an average of 0.55 times the average Sq£ during their two seasons, finishing 19th (1 spot above relegation) in 1993 and 21st (and relegated) in 1994. The average finish of 20th given their MSq£ represents the largest underachievement of any club in the Premier League’s history.
Analysis of how to improve one’s Champions League qualification chances can now be studied as there is a basic understanding of PI’s.
As previously discussed, the regression equation predicted a club with an MSq£ of 1.98 had a 50/50 chance of finishing fourth or better. How great of a squad cost is required to achieve a 75% chance (or 3-to-1) of qualifying for Champions League? If one thinks in terms of PI’s, the corresponding PI would be the one where the upper bound leaves 25% of the data outside of the distribution. If PI’s are equally distributed around the regression equation and one wants to find the PI with an upper bound that leaves 25% of the data outside of the distribution, the corresponding PI is the 50% PI. The MSq£ where the 25% upper bound from the PI equals 4.0 is 2.26. This means teams that spend 2.26 the average squad cost will have 3-to-1 odds of finishing fourth or better.
Using various PI’s, the following MSq£’s are required to achieve the corresponding odds of finishing fourth or better.
- 3-to-1 odds for: MSq£=2.26
- 5-to-1 odds for: MSq£=2.38
- 10-to-1 odds for: MSq£=2.55
Looking at the historical record, these odds are achieved at much lower expenditure multiples. Since the 2001-02 season any team that has had an MSq£ of 2.12 or greater has qualified for the next season’s Champions League. In fact, only one team has had an MSq£ of 1.98 or greater and failed to qualify for Champions League - Manchester City in 2009-10 (Spurs’ and their 1.68 MSq£ nipped them for fourth). Everton owns the lowest MSq£ for a Champion’s League qualifier, with their fourth place finish in 2004-05 supported by an MSq£ of 0.74 (note: they subsequently failed to make it out of the Champions League third qualifying round). One must climb another thirty-seven positions in the MSq£ rankings since 2001-02 to find the next Champions League qualifier – Arsenal’s 2008-2009 squad with an MSq£ of 1.01. Odds improve to 50/50 around an MSq£ of 1.60 to 1.65. It seems as if this is the perfect example of the over prediction phenomenon that Stefan Szymanski wrote about. Keep this in mind when the financial improvement needed at Liverpool is discussed.
It is now becoming clear as to how much more Liverpool must spend to improve their odds of qualifying for Champions League in the 2010-2011. Based upon the regression model predictions, they must spend the following sums to achieve the given odds:
- Even odds: £73.6M
- 3-to-1 odds for: £105.3M
- 5-to-1 odds for: £119.2M
- 10-to-1 odds for: £138.8M
So now that the cost to compete for Champions League positions is understood, how should a team or manager be evaluated against those odds? What about the other sixteen teams in the league that do not qualify for such a competition - how should they and their managers be judged? A framework to aid such judgement will be discussed in the second post in this series, and it will also be applied to a number of managers to determine who has under and over performed the most given the financial resources expended by the club.
Editorial Note: Readers who had access to the original version of this post may notice a change in the second graph between the original post and this one. In that first post I mistakenly labeled the left-hand y-axis of the graph as "Average Sq£". It should have been labeled "Average £XI" as that was the data shown in the plot. The graph in this post, and the first sentence of commentary after it, has been corrected to plot the average Sq£ per the label on the left-hand y-axis. The core conclusion of that portion of the original post, that an increasing share of squad transfer costs are going unused during a season, is unchanged as that data was correctly plotted.



No comments:
Post a Comment